Расчет температурного поля откоса
Информационный портал
ТЕМПЕРАТУРНЫХ ПОЛЕЙ МЕТОДОМ СЕТОК И ГРАФИЧЕСКИМ МЕТОДОМ
Рассмотрим два метода, которые могут быть сравнительно просто использованы в инженерной практике для расчета двумерных температурных полей конструкций.
Метод сеток. Область двумерного сечения конструкции, для которой требуется построить температурное поле,
Делят на элементарные площадки, центры которых соединяют сосредоточенными термическими сопротивлениями (рис. III.14, А). Таким образом, переходят от поля к тепловой сетке (рис. III. 14, Б) с сосредоточенными параметрами [II 1.9].
Уравнение стационарной теплопроводности для такой сетк^ (поле однородное) в конечных разностях имеет вид
Вторые конечные разности приращения температуры в направлениях Х Alt и У Ay2t соответственно равны:
Решение уравнения (III.53) относительно температуры в произвольном узле сетки T0 (рис. III.14, б), если шаг сетки в направлении Х, Ах и У, Ау, одинаковый, может быть получено в виде
Таким образом, при однородном поле температура в произвольном узле сетки равна среднеарифметическому значению температуры в соседних узлах.
Для конструкции неоднородной и с произвольным шагом разбивки сетки решение конечноразностного уравнения относительно To Имеет вид
Где K„-i> /t0_2, К0-з и Ko-i — показатели проводимости соединений тепловой сетки (их определение для наиболее сложных случаев показано на рис. III.15 и III.16) между соответствующими узлами в центрах элементарных площадок.
Из уравнения (II 1.55) следует, что в общем случае температура в произвольном узле равна средневзвешенному (по проводимостям связей) значению температур в соседних узлах. Это общее уравнение может быть использовано в том числе для определения температуры в узлах, граничащих с поверхностью ограждения (рис. III.16), а также в узлах на стыках материальных слоев (см. рис. II 1.15).
Показатель проводимости К между узлами должен определяться по правилу сложения параллельно и последовательно расположенных термических сопротивлений R (см. рис. III.16). Может быть два слу
Чая определения термических сопротивлений. Сопротивление теплопроводности однородного объемного элемента равно
Где I — протяженность элемента в направлении, в котором определяется сопротивление; F — площадь элемента в сечении, перпендикулярном этому направлению.
Сопротивление теплообмену на поверхности элемента, граничащего с воздухом, равно
Где А — коэффициент теплообмена на этой поверхности; F — площадь поверхности элемента.
Разбивку на элементарные блоки, в центре которых будут расположены узлы тепловой сетки, лучше проводить так, чтобы их границы совпадали с характерными поверхностями в сечении ограждения. Чем мельче разбивка, тем выше точность расчета, но тем сложнее и медленнее его продвижение.
Расчет состоит в решении системы линейных уравнений, состоящей из стольких уравнений, сколько узлов в принятой тепловой сетке. Систему уравнений удобнее всего решать методом последовательного приближения, сущность которого в следующем. Сначала задают ориентировочные значения температур в узлах тепловой сетки, затем постепенно уточняют эти значения, добиваясь удовлетворения уравнений системы.
В теории методов приближенных вычислений рассматривается ряд приемов таких расчетов, которыми можно пользоваться в данном случае. Наиболее удобным является метод релаксации, который со-
Стоит в определении дебаланса в каждой точке с постепенным его уменьшением и доведением до величин, близких к нулю, изменением температуры в данной и соседних точках.
Для простейшего случая однородной конструкции дебаланс в узле At из уравнения (II 1.54) можно записать в виде
Из этого уравнения видно, что изменением температуры в каждой из соседних точек (/, 2, 3, 4) на единицу можно скорректировать At
На±1, а изменением температуры в узловой точке (0) — на±4. Это обстоятельство является, по существу, ключом к последовательности вычислений (рис. III.17). После задания в узлах ориентировочных температур и вычисления At изменяют температуры, начиная с узлов наибольшего дебаланса и, перемещаясь от узла к узлу, уменьшают его.
Методом сеток можно вести расчеты для случаев практически любой сложности-и в том числе с источниками или стоками тепла в цилиндрической системе координат и др. Однако ручной расчет температурных полей методом сеток достаточно трудоемок, поэтому для его реализации в настоящее время широко используется ЭВМ.
Графический метод. Метод графического приближенного построения (от руки) стационарного двумерного температурного поля удобен для получения сравнительно быстрого ориентировочного представления о сложном поле. Этот метод основан на построении ортогональной сетки криволинейных — квадратов, образованной линиями токов тепла и изотермами. Рисуются линии токов тепла и изотермы в виде ортогональной сетки криволинейных квадратов (рис. III. 18), т. е. такой сетки, линии которой ортогональны (т. е. в точках пересечения образуют прямые углы) и в которой в пределах каждого квадрата среднее расстояние между изотермами равно среднему расстоянию между линиями токов тепла:
А /х = Д 1г.
В. такой сетке поток тепла в «трубке», образованной двумя линиями тока, равен
Т, и т2 — температуры на границах области, для которой строится температурное поле; S — число интервалов между изотермами.
Если число «трубок» тока (интервалов между линиями тепловых потоков) в пределах рассматриваемой области (части конструкции) обозначить через Б, то общее количество тепла, проходящее через эту часть конструкции, будет равно
А сопротивление теплопроводности этой части R?
Фактор формы. Отношение Б/S в формуле (111.62) является геометрическим параметром, характеризующим область (двумерного температурного поля) определенной конфигурации. Для одномерного поля стенки с шириной поверхности в один калибр (один калибр равен толщине стены) Б/S = 1, а шириной поверхности в два калибра равно 2 и т. д. Для двумерной области с такой же шириной поверхности эти отношения другие. Отношение геометрических параметров ¦для двумерной и одномерной областей одинаковой ширины показывает, во сколько раз изменяется тепловой поток через поверхность определенной ширины в двумерной области по сравнению с одномерной.
Обычно угол, стык, откос, включение и другие изменения в одномерной конструкции вызывают нарушение одномерности температурного поля на расстоянии до двух кальбров по ширине ограждения, поэтому для всех случаев двумерных полей в ограждении необходимо учитывать участок ограждения шириной в два калибра.
За один калибр для реальных ограждений (многослойных, имеющих конечные значения сопротивлений теплообмена) принимают условную толщину однородного ограждения с сопротивлением теплопроводности R0 и коэффициентом теплопроводности теплоизоляционного материала к. Ширина Af в два калибра Равна
При расчете передачи тепла через двумерные элементы в ограждении (участки конструкций с двумерным температурным полем) удобно пользоваться так называемым фактором формы. Фактором формы / двумерного элемента ограждения называется отношение геометрических параметров Б/5 двумерной и одномерной частей ограждения при их одинаковой ширине по поверхности, равней двум калибрам:
Где Б/S — отношение числа трубок тока к числу изотермических полос (интервалов между изотермами) в ортогональной сетке криволинейных квадратов, расположенных в области двумерного темпе-г ратурного поля на ширине поверхности в два калибра; 2 —это же отношение для области одномерного температурного поля в конструкции при той же ширине поверхности в два калибра.
Фактор формы показывает, во сколько раз больше проводимость тепла двумерным элементом по сравнению с одномерным. Или при одинаковой разности температур и прочих условиях он показывает, во сколько раз больше теряется тепла через двумерный элемент ограждения по сравнению с теплопотерями через его гладь.
Для некоторых двумерных элементов (угла, стыка ограждений) фактор формы может быть вычислен относительно внутренней и наружной поверхностей. В расчете потерь тепла помещением площади ограждений принимают по наружному обмеру; в этом случае / следует определять по наружной поверхности.
Двумерное температурное поле
Условия теплообмена на откосах простенков, в наружных углах зданий и в местах примыкания к внешним ограждениям поперечных стен или перегородок искажают одномерное температурное поле, изотермы теряют параллельность, а поток тепла одномерность.
При теплотехнических расчетах достаточно исследовать температурное поле в двух измерениях х и у, а в направлении z (обычно принимается не менее 1 м) принять температуру постоянной, то есть рассматривать температурное поле в плане или разрезе. Такое поле является плоским. На рис. 6.2 показан пример температурного поля во внешнем углу.
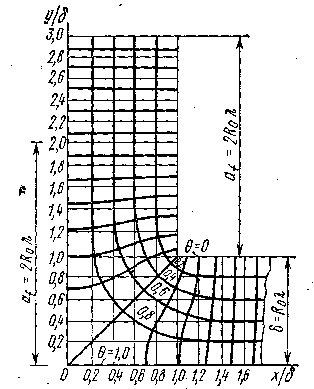 |
Рис. 6.2 — Пример плоского двухмерного температурного поля во внешнем углу
В однородной материальной среде температурное поле описывается уравнением
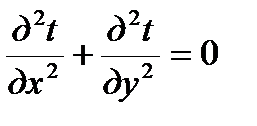 . (6.6)
. (6.6)
В неоднородной материальной среде уравнение имеет вид
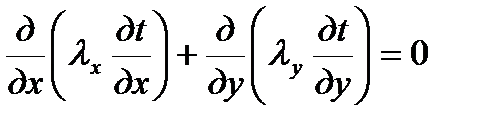 . (6.7)
. (6.7)
Здесь λ является непрерывной функцией координат х и у.
В практических расчетах используется метод конечных разностей, что дает возможность заменить непрерывное значение λ скачкообразным. Применение этого метода связано с нанесением на рассматриваемую проекцию конструкции расчетной сетки, которая позволяет вычислить температуры в ее узлах. Сетка выбирается, как правило, квадратной со стороной Δ. Желательно, чтобы узлы сетки совпадали с поверхностями ограждения. Чем меньше величина Δ, тем точнее расчет.
Расчет заключается в определении температуры (txy) в точке через значения температур, окружающих эту точку со значениями температур (t1, t2, t3, t4). Эта точка обменивается с ними следующими количествами тепла
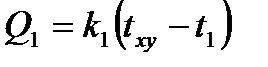 ;
; 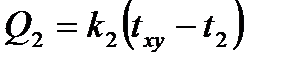 ;
; 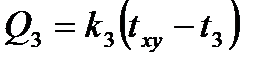 ;
; 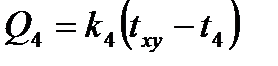 . (6.8)
. (6.8)
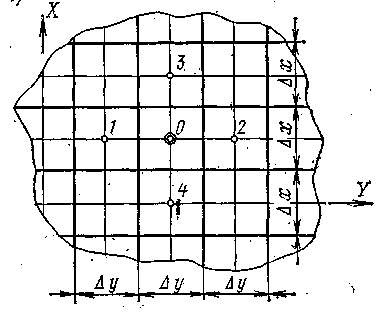
Рис. 6.3 — Схема передачи тепла между узлами сетки
В условиях теплового баланса сумма этих количеств тепла равна 0, т.е.
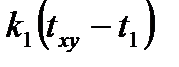 +
+ 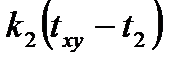 +
+ 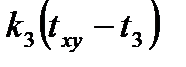 +
+ 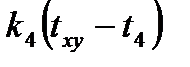 = 0. (6.9)
= 0. (6.9)
Отсюда определяется температура в расчетной точке
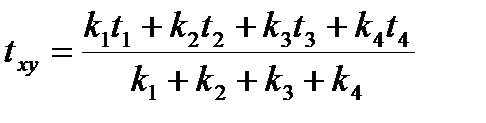 , (6.10)
, (6.10)
где k1, k2, k3, k4 — коэффициенты теплопередачи в направлении соответствующих точек. Если конструкция однородная, то расчет ведется по формуле
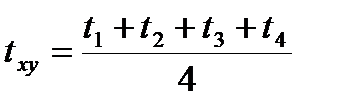 . (6.11)
. (6.11)
Коэффициент теплопередачи определяется исходя из условия, что передача теплоты происходит по квадрату со стороной Δ. Если материал однородный, то 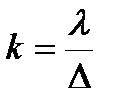 , при наличии двух материалов
, при наличии двух материалов 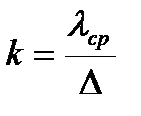 (
( 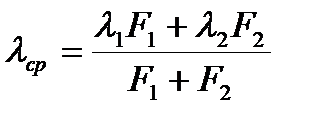 — осредненная по площадям F1 і F2 теплопроводность).
— осредненная по площадям F1 і F2 теплопроводность).
Если материал неоднороден, то принимается
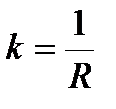 .
.
Коэффициент теплоотдачи между узлами, которые лежат на поверхности, граничащей с воздухом, находится как 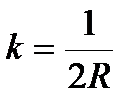 , поскольку передача тепла происходит только по 0,5Δ.
, поскольку передача тепла происходит только по 0,5Δ.
Температура в углу
В углу температура всегда ниже температуры внутренней поверхности по основному полю внешней стены. Такое явление происходит по двум причинам. Во-первых, к углу подача тепла через конвекцию ограничена, из-за необходимости преодолевать сопротивление пристенного ламинарного воздушного слоя. Во-вторых, площадь восприятия тепла в углу значительно меньше площади теплоотдачи наружному воздуху.
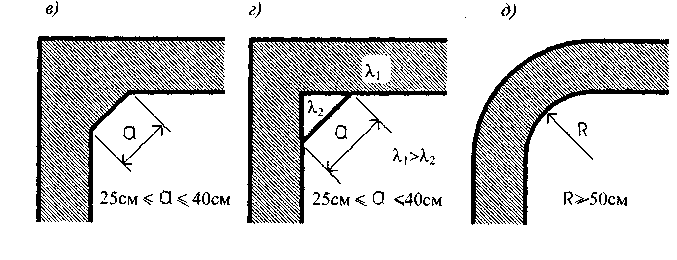 Конструктивно увеличить температуру в углу возможно за счет способов, некоторые из которых приведены на рис. 6.4.
Конструктивно увеличить температуру в углу возможно за счет способов, некоторые из которых приведены на рис. 6.4.
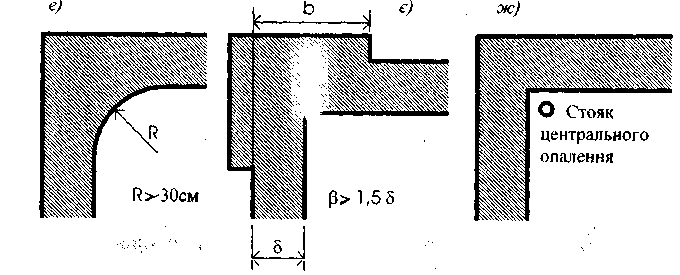
Рис. 6.4 — Способы утепления наружного угла
39. Расчет на температурные воздействия в ЛИРА 10.6
Расчет на температурные воздействия – задача достаточно непростая и встречающаяся не так часто, поэтому у рядового проектировщика могут возникнуть трудности с моделированием такого типа воздействия, особенно в первый раз. Исходя из этого в сегодняшней заметке коснемся плотнее этого вопроса и разберем подробнее не только тонкости задания температурных нагрузок в ЛИРА 10.6, но и положения норм.
Температурные воздействия на строительные конструкции имеют самое разнообразное происхождение, но чаще всего учитываются климатические температурные нагрузки и технологические температурные воздействия, реже рассматриваются воздействия, обусловленные пожарами.
Рассмотрим нормативные документы, в которых говорится о необходимости проведения расчетов на температурные воздействия.
В п. 1.15 пособия по проектированию жилых зданий (к СНиП 2.08.01-85) говорится: в протяженных в плане зданиях, а также зданиях, состоящих из объемов разной высоты, рекомендуется устраивать вертикальные деформационные швы: температурные — для уменьшения усилий в конструкциях и ограничения раскрытия в них трещин вследствие стеснения основанием температурных и усадочных деформаций бетонных и железобетонных конструкций здания. При этом, если обратиться к таблице 3 того же документа, в ней мы найдем максимально допустимые расстояния между температурно-усадочными швами в зависимости от конструктивной системы зданий. Например, для перекрестно-стеновой системы с несущими наружными и внутренними стенами в монолитных зданиях это расстояние не должно превышать 40 м. В случаях, когда эти значения превышаются, требуется производить расчет на температурные воздействия.
Еще одним похожим документом, в котором говорится о необходимости проведения расчетов на температурные воздействия, является «Пособие по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительно напряжения арматуры» (к СНИП 2.03.01-84), п. 1.19.
Но в этих документах ничего не говорится непосредственно о величинах и способах задания температурных воздействий. Эта информация содержится в основном своде правил расчетчика — СП 20.13330.2011, раздел 13 «температурные климатические воздействия».
Для расчета на температурные воздействия в ЛИРА 10.6 реализованы 2 способа задания температурных нагрузок как для пластинчатых КЭ, так и для стержневых, которые позволяют смоделировать любое температурное воздействие:
Когда температура на верхних и нижних волокнах симметричного сечения одинакова по величине и по знаку, это аналогично равномерному расширению/сжатию волокон вдоль оси стержня, что вызывает в случае статически неопределимой системы напряжения растяжения или сжатия, либо соответствующие деформации в случае статически определимой системы.
Если же стержень подвержен действию перепада температуры, то более нагретые волокна его сечения будут сжаты, а менее нагретые – растянуты – это температурный изгиб. В случае статически определимой системы будут возникать лишь деформации.
Следует отметить, что принцип задания температурных воздействий в ЛИРА 10.6 несколько отличается от предписания норм и носит универсальный характер. Расчетчик всегда должен понимать какое напряженно деформированное состояние вызовет то или иное температурное воздействие и, исходя из этого, выбирать нужный тип нагрузки.
В качестве примера разберем простую задачу расчета прямоугольной плиты. Плита расположена на открытой местности, следовательно, подвергается воздействию солнечной радиации, что вызывает температурный изгиб. Также будем считать, что плита подвергается равномерному нагреву/охлаждению. Район строительства – Московская область. Габариты — 20х30 м, толщина плиты — 1 м. Эти параметры необходимы для принятия температурных характеристик, которые регламентирует СП «Нагрузки и воздействия».
Согласно п. 13.2 СП 20.13330.2011, определим нормативные значения изменений средних температур по сечению элемента в теплое и холодное время года.
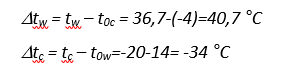
Нормативные значения средних температур tw и tc в теплое и холодное время года для однослойных конструкций определяем по таблице 13.1 СП 20.13330.2011.
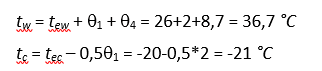
t0w, t0c — начальные температуры в теплое и холодное время года, принимаемые в соответствии с 13.6 СП.
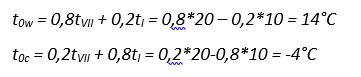
tew, tec – средние суточные температуры наружного воздуха соответственно в теплое и холодное время года, принимаемые в соответствии с п. 13.4.
θ1 = 2°С, — приращение средних по сечению элемента температур и перепада температур от суточных колебаний температуры наружного воздуха, принимаемые по таблице 13.2.
θ4 = 0,05ρ Smaxk = 0,05*0,7*830*0,3 = 8,7 – приращения средних по сечению элемента температур и перепада температур от солнечной радиации, принимаемые в соответствии с 13.5.
Средние суточные температуры наружного воздуха в теплое tew и холодное tec время года определяем по формулам:
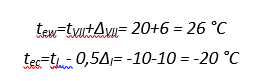
где tI= -10°С, tVII = 20 °С – многолетние средние месячные температуры воздуха в январе и июле, принимаемые соответственно по картам 5 и 6 приложения Ж.
ΔVII = 6°С, ΔI = 20 °С отклонения средних суточных температур от средних месячных (ΔI принимается по карте 7 приложения Ж).
Перепады температур по сечению элемента в теплое ϑw и холодное ϑс время года определяются по таблице 13.1:
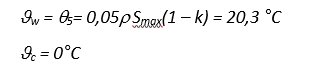
Коэффициент надежности по нагрузке γf для температурных климатических воздействий Δt и ϑ принимается равным 1,1.
Из всех приведенных выше вычислений нас интересуют 2 величины: нормативные значения средних температур по сечению элемента в теплое и холодное время года Δtw, Δtc и перепады температур по сечению элемента в теплое ϑw и холодное ϑc время года. Далее у расчетчиков возникают сложности с трактовкой норм, какую из приведенных величин задавать. В СП 20.13330.2011 явно это нигде не прописано. Вообще, стоит отметить, что данную информацию сложно найти в какой-либо литературе. На помощь нам пришла работа [4], в которой эта информация содержится, хотя и не явно.
Температурные усилия возникают только в статически неопределимых конструкциях. Для систем с одной лишней связью эти усилия возникают после превращения конструкции в статически неопределимую, то есть после замыкания системы. Замыкание системы реализуется при некоторой температуре t – температуре замыкания системы. Отсюда становится понятным смысл величин Δtw и Δtc. При задании равномерного нагрева/охлаждения, расчетчик должен знать, в какое время года будет замкнута (построена) конструкция. То есть, если конструкция построена (замкнута) зимой, в качестве нагрузки выбираем Δtw и наоборот. Но это в идеализированном случае. На практике же большая часть сооружений относится к системам с множеством лишних связей, замыкание которых происходит в различные моменты времени. Для таких конструкций нельзя точно определить температуру замыкания, которой соответствовали бы нулевые усилия. Уже в процессе строительства возникают температурные деформации и усилия, зависящие как от климатических условий, так и от последовательности монтажа. Логично предположить, что начальные усилия, возникающие в процессе строительства, имеют меньшие значения, чем температурные усилия после полного замыкания системы. При многоступенчатом замыкании конструкции происходит распределение во времени возникновения усилий, поэтому допустимо было бы принимать в качестве температуры t значение, являющееся средним за период строительства. В СП же приведены значения, которые позволяют учесть только один момент замыкания, следовательно, можно сделать вывод, что, принимая значения, регламентированные СП, мы учитываем нагрузку в запас.
Исходя из вышеизложенного, при расчете на температурные воздействия для нашего примера необходимо создавать три температурных загружения:
Загружение 1. Равномерный нагрев на величину Δtw, что соответствует зимнему периоду замыкания.
Загружение 2. Равномерное охлаждение на величину Δtс, что соответствует летнему замыканию конструкции.
Загружение 3. Температурный изгиб, определяемый перепадом температур ϑw в теплое время года.
Отметим, что в другом примере, в случае отличия величины ϑс от нуля, необходимо бы было задавать еще одно загружение. Кроме этого, загружения 1 и 2 не могут действовать одновременно, поэтому необходимо указать их взаимоисключение.
Обратимся теперь непосредственно к заданию температурных нагрузок в ЛИРА 10.6.
В случае загружений 1 и 2 все достаточно тривиально, мы лишь задаем соответствующее значение в поле нагрузки (рис. 1).
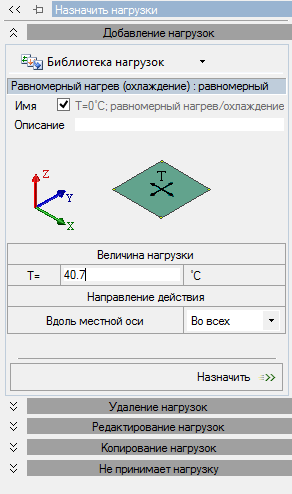
Рис. 1. Задание равномерного нагрева
Как говорилось выше, в данном примере речь идет о температурном изгибе, в режиме задания нагрузок выбираем нагрузки на пластины – температурный изгиб (рис. 1).
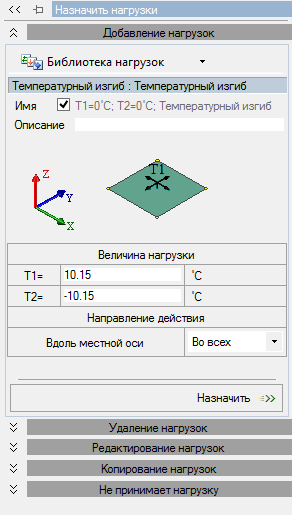
Рис. 2. Окно задания температурного изгиба
Так как для холодного периода времени ϑc = 0°С, расчет на температурный изгиб будем производить только для теплого времени года.
Т1 –температура верхнего волокна, нагретого солнцем; Т2 – температура нижнего волокна, следует учитывать, что положение волокон зависит от направления местной оси Z1 элементов. Направление действия выбираем «Во всех», это означает, что материал расширяется равномерно по оси Y и X.
Остается нераскрытым самый главный вопрос: как сопоставить значения различных вычисленных по СП характеристик температурных воздействий с тем, что нужно задавать в ПК ЛИРА.
В случае температурного изгиба значение имеет разность температур, при этом, логично, что верхние волокна должны иметь большую температуру, чем нижние. Поэтому тут принимаем:
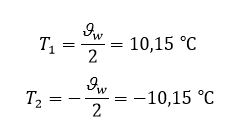
Эти значения вводим в соответствующие поля в программе (рис. 2).
Стоит отметить, что при задании температурных нагрузок плиту следует закреплять «крестом», как показано на рисунке 3. Это объясняется тем, что при задании закреплений как в задачах без температурного расчета, вследствие расширения материала будут возникать дополнительные сжимающие/растягивающие усилия, которые в реальности не будут наблюдаться, т.к. плита может проскальзывать по грунту.

Рис. 3. Закрепление плиты
Картина распределения моментов от температурного загружения приведена на рисунке 4.
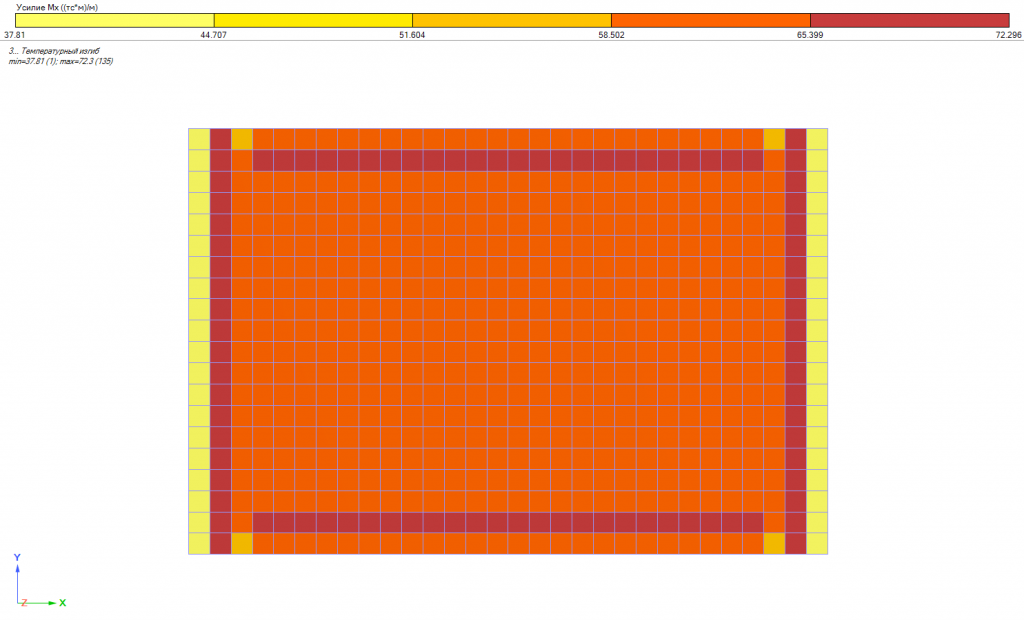
Рис. 4. Мозаика моментов от температурного изгиба
Таким образом, мы рассмотрели весьма непростой вопрос расчета на температурные воздействия. Еще остается открытой задача расчета температурных полей. Подробнее эта тема будет раскрыта в предстоящем вебинаре.
Использованная литература:
- СП 20.13330.2011 Нагрузки и воздействия.
- Пособие по проектированию жилых зданий Вып. 3 (к СНИП 2.08.01-85)
- Пособие по проектированию бетонных и железобетонных конструкций из тяжелого бетона без предварительного напряжения арматуры (к СП 52-101-2003)
- В.Н. Гордеев, А.И. Лантух-Лященко, В.А. Пашинский, А.В. Перельмутер, С.Ф. Пичугин. Нагрузки и воздействия на здания и сооружения. – М: Издательство Ассоциации строительных вузов, 2007.
Расчет температурного поля откоса

- О компании
- О нас
- Главная
- Реквизиты
- Презентационный каталог
- Свидетельства
- О нас
- Услуги
- Энергетическое обследование (энергоаудит)
- Энергосервис
- Энергетический паспорт объекта
- Тепловизионное обследование зданий и сооружений
- Техническое обследование зданий и сооружений
- Контроль кратности воздухообмена
- Технический заказчик
- Строительный контроль
- Пусконаладоные работы и электролаборатория
- Проектирование
- Расчет температурных полей конструкций
- Продажа оборудования для энергоаудита
- Наши объекты
- Тепловизионное обследование зданий и сооружений
- Энергетическое обследование (энергоаудит)
- Техническое обследование зданий и сооружений
- Измерение воздухопроницаемости и кратности воздухообмена
- Технический заказчик
- Строительный контроль
- СРО в энергетике
- Условия вступления
- Обучение
- Экспертиза энергопаспорта
- Оборудование
- Вакансии
- Контакты
- Пассивный дом (энергосберегающий дом)
- Расчет температурных полей конструкций
- Ограждающие конструкции
Расчет температурных полей конструкций
В связи с истощением природных энергетических запасов возрастает актуальность проблемы экономии топливно-энергетических ресурсов и повышения энергоэффективности зданий. Для решения этой задачи необходимо проведение различных энергосберегающих мероприятий: применение эффективных и экологически безопасных теплоизоляционных материалов; использование энергоэкономичных, надежных и долговечных ограждающих конструкций, снижение теплопотерь; повышение качества теплотехнического проектирования зданий.
В настоящее время согласно нормам СНиП 23-02-2003 «Тепловая защита зданий» установлены три показателя тепловой защиты здания:
«а» Приведенное сопротивление теплопередаче отдельных элементов ограждающих конструкций здания.
«б» Санитарно-гигиенической ,включающий температурный перепад между температурами внутреннего воздуха и на поверхности ограждающих конструкций и температуру на внутренней поверхности выше температуры точки росы
«в» Удельный расход тепловой энергии на отопление здания
Требования тепловой защиты здания будут выполнены, если в жилых и общественных зданиях будут соблюдены требования показателей «а» и «б» либо «б» и «в».Требования показателей «б» должны отвечать все виды ограждающих конструкции: обеспечивать комфортные условия пребывания человека и предотвращать поверхности внутри помещения от увлажнения, намокания и появления плесени.
Методы и пути достижения этих нормируемых показателей выбираются и обеспечиваются при проектировании. В реальном проектировании влияние теплопроводных включении (мостиков холода) на теплозащитные свойства и энергоэффективность зданий , как правило, не учитывается. Проектировщики необоснованно используют завышенные значения коэффициентов теплотехнической однородности, по которым и определяется значения приведенного сопротивления теплопередаче ограждений. Это является основой для иллюзии о достигнутом высоком уровне теплозащиты.
Полноценные расчеты значений приведенного сопротивления теплопередаче конструкций, коэффициентов теплотехнической однородности, температур на внутренней поверхности ограждающих конструкции при проектировании зданий согласно СНиП 23-02-2003 «Тепловая защита зданий» и СП 23-101-2004 «Проектирование тепловой защиты зданий» должны выполнятся на основе расчета температурных полей. Необходимость такого рода в первую очередь связана с обеспечением безопасности функционирования здания, предотвращения промерзания, увлажнения , появления плесени на внутренней поверхности ограждающих конструкции в зоне теплопроводных включений (наружные углы, стыки, оконные откосы),а также сократить теплопотери через указанные места. Расчеты температурных полей помогают заблаговременно (на стадии проектирования) избежать теплотехнических дефектов.
Расчет температурного поля в многослойной конструкции
Определим температуры на границах слоёв многослойной конструкции наружной стены, тепловой поток и глубина промерзания при следующих данных: 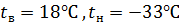
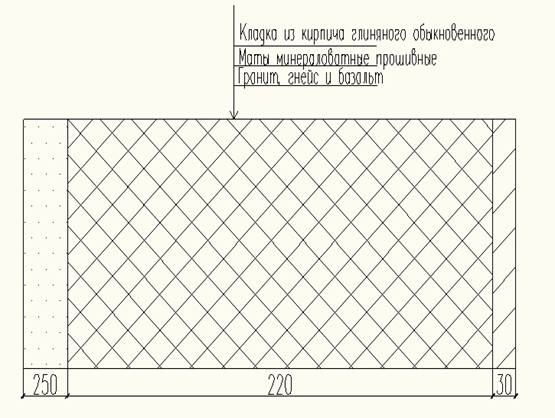
Рисунок 2.1 – Наружная стена здания
— Кладка из кирпича глиняного обыкновенного(Д)
— Маты минераловатные прошивные (А)
— Гранит, гнейс и базальт (В)
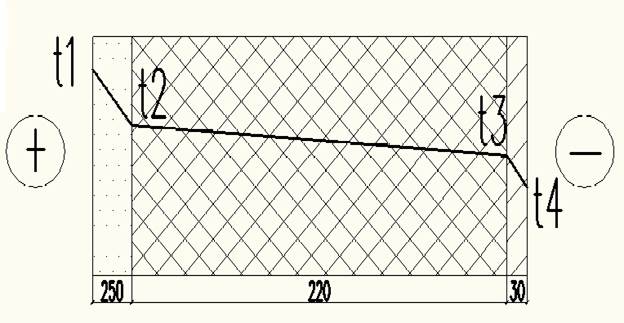
Рисунок 2.2 – Изменение температуры в наружной стене
Определяем термическое сопротивление каждого слоя материала:
Для определения тепловой инерции стены находим термическое сопротивление отдельных слоев конструкции по формуле:
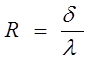 ,
,
где δ – толщина рассматриваемого слоя, м ;
λ – коэффициент теплопроводности данного слоя, Вт/(м∙°С).
Вычислим термическое сопротивление отдельных слоев:
— Кладка из кирпича глиняного обыкновенного
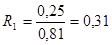 (м 2 ∙ ºС)/Вт;
(м 2 ∙ ºС)/Вт;
— Маты минераловатные прошивные
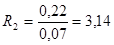 (м 2 ∙ ºС)/Вт;
(м 2 ∙ ºС)/Вт;
— Гранит, гнейс и базальт
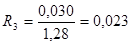 (м 2 ∙ ºС)/Вт;
(м 2 ∙ ºС)/Вт;
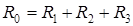 =0,31+3,14+0,023=3,473 (м 2 ∙ ºС)/Вт.
=0,31+3,14+0,023=3,473 (м 2 ∙ ºС)/Вт.
Вот тут Штирлиц чего-то не понял. А принимали, вроде, 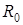 =3,2? По слоям уточнить!
=3,2? По слоям уточнить!
Определим тепловой поток через трехслойную конструкцию при разности температур двух сред:
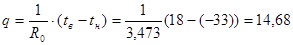 Вт/м 2 ,
Вт/м 2 ,
где tв — температура внутреннего воздуха, °С;
tн — температура наружного воздуха, °С .
Определяем температуры на границах слоев конструкции по формуле:
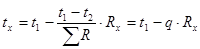 ,
,
где tx — температура в любой точке конструкции, °С;
Rx — часть термического сопротивления, находящегося между плоскостями c температурами t1 и tx, (м 2 ∙ ºС)/Вт.
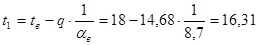 ºС;
ºС;
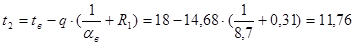 ºС;
ºС;
 ºС;
ºС;
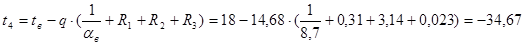 ºС;
ºС;
Граница промерзания находится в слое «маты минераловатные прошивные».
Определяем глубину промерзания в теплоизоляционном слое и составляем пропорцию:
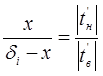
 ;
;
Общая глубина промерзания в этом случае составит:
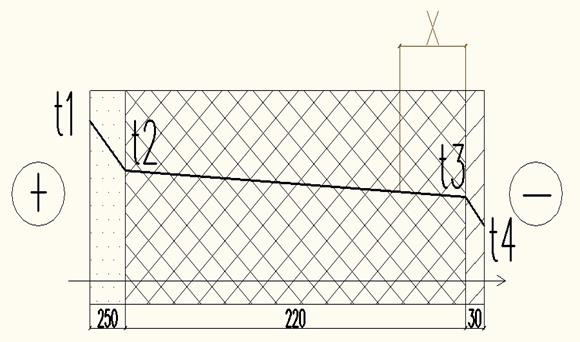
Рисунок 2.2 – Глубина промерзания в теплоизоляционном слое
Рассмотрим данную задачу в случае, когда температура наружного и внутреннего воздуха поменяны друг с другом .
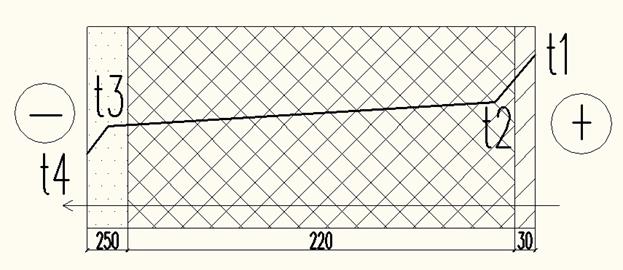
Рисунок 2.3 — Изменение температуры в наружной стене
Температурное поле на этом рисунке имеет совершенно загадочные перегибы. С чего бы?
Значение термического сопротивления всей конструкции и теплового потока в этом случае останется прежним:

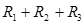 =0,31+3,14+0,023=3,473 (м 2 ∙ ºС)/Вт.
=0,31+3,14+0,023=3,473 (м 2 ∙ ºС)/Вт.
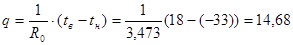 Вт/м 2 .
Вт/м 2 .
Определяем температуры на границах слоев конструкции по формуле:
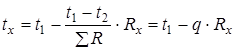 ,
,
где tx — температура в любой точке конструкции, °С;
Rx — часть термического сопротивления, находящегося между плоскостями c температурами t1 и tx, (м 2 ∙ ºС)/Вт.
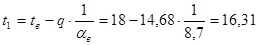 ºС;
ºС;
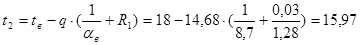 ºС;
ºС;
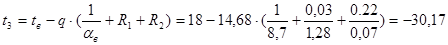 ºС;
ºС;
 ºС;
ºС;
Граница промерзания находится в слое «маты минераловатные прошивные».
Определяем глубину промерзания в теплоизоляционном слое и составляем пропорцию:
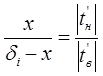
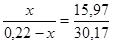 ;
;
Общая глубина промерзания в этом случае составит:
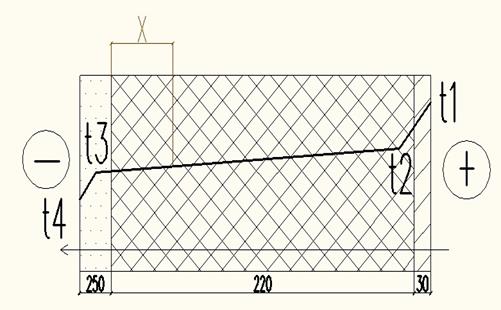
Рисунок 2.4 – Глубина промерзания в теплоизоляционном слое
Откорректить рисунок в соответствии со здравым смыслом. И с физическим тоже!
Вывод: Глубина промерзания, в первом случае составляет 90 мм, во втором случае 380 мм. Экономически целесообразнее делать теплоизоляция как представлено в первом случае, при этом точка росы переносится в теплоизоляционный слой и стена незначительно промерзает в отличие от теплоизоляция, которая представлена во втором случае. При наружной теплоизоляции ограждающая конструкция аккумулирует тепло, потери тепла минимальны.
Трудно вам, бедным. У всех общий папа чукча…На русский переведи. Или на английский — лишь бы предлоги с падежами согласовывались



